【導讀】近有一系列基于 PWM 信號“處理器”主題的設計思想發表。這些處理器的目的是限度地減少響應 PWM 占空比變化的建立時間和殘余 PWM 紋波。在許多情況下,更簡單的處理器(僅由一個由電阻器和電容器構建的低通濾波器組成)表現良好(圖 1)。
近有一系列基于 PWM 信號“處理器”主題的設計思想發表。這些處理器的目的是限度地減少響應 PWM 占空比變化的建立時間和殘余 PWM 紋波。在許多情況下,更簡單的處理器(僅由一個由電阻器和電容器構建的低通濾波器組成)表現良好(圖 1)。
用您獨特的設計讓工程界驚嘆不已: 設計創意提交指南
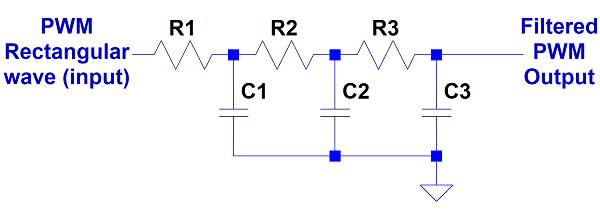
圖 1帶有低通濾波器的簡單 PWM 處理器,該低通濾波器由電阻器和電容器構成,該濾波器結構只能實現實極點。
然而,關于如何為任意特性的PWM選擇濾波器元件值的討論很少,更不用說針對一種想法中提到的特定PWM(8位,1MHz時鐘)。在本文中,我將介紹一種針對任意周期 PWM 優化這些更簡單濾波器的方法。
讓我們從一些術語開始:我們將未過濾的 PWM 描述為具有 B 位、占空比 d、周期 T 和(無單位)輸出值 0 或 1。(警告:如果您只想解決問題并且不想體驗推導的快感和數學的痛苦,請跳至本文末尾的“實施解決方案”部分。)
對于具有負、不等極點 p1、p2 和 p3 的任何三階濾波器,單位階躍的時域響應為:
如果兩個或三個極點相等,則響應不同。對于三個,它是:
![]()
我們的興趣之一是穩定到 1 的指定分數 F 所需的時間 (t s )(從 d = 0 到 1 的滿量程 PWM 轉換的壞情況)。處理幅度穩定誤差 (ASE),h(t, p1, p2, p3) = 1 – hh(t, p1, p2, p3)。ASE 在時間 t = 無窮大時完全穩定(歸零)。我們可能會詢問 t s的值,使得 h(t s ,p1,p2,p3) = F = 2 -B-1或 PWM 的 ? LSB。當然,如果應用程序產生更小的占空比階躍,則可以做出其他選擇。
我們還對過濾后的 PWM 紋波的幅度感興趣。濾波器的頻率響應為:
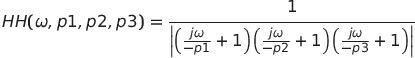
其中 j = (√-1),ω 是以弧度/秒 (rad/sec) 為單位的頻率。
未濾波的 PWM 輸出可以表示為頻率為 1/T = ω PWM /(2π) Hz整數倍的無限多個正弦波的總和。當 d = 50% 且頻率為 ω PWM弧度/秒時,可產生的幅度正弦波具有 2/π 的峰值幅度。整個 PWM 信號通過一個低通濾波器,該濾波器比個衰減更高的倍數。在這些條件下,相當好的低通濾波器的輸出幾乎完全由 ω PWM的頻率組成。顯然,過多的紋波和過多的穩定時間同樣會毀掉您的一天。所以我們想知道 ω PWM和 t s對于 ASE 和紋波幅度都等于 F 的濾波器,即它們滿足 H(ω PWM , p1, p2, p3) = π?HH(ω PWM , p1, p2, p3 )/2 = F 且 F = h(t s , p1, p2, p3)。當然,我們還想找到對于給定的 F 值能為我們提供 t s和 ω PWM的濾波器。
讓我們首先看一下 PWM 的具體情況,其值為 T = 2 8 /1 MHz = .000256,其中 ω PWM = 2π/T = 24543。一個明顯的起點是等值電阻器和電容器的濾波器。對于圖 1 電路,頻率響應傳遞函數為:
![]()
將每個 R 設置為 1 Ω,將每個 C 設置為 1 F,多項式求根例程可用于確定滿足 H() = F = 2 -8-1 : -3.247, -1.555的三個極點和 ω 的值, -.1981 和 9.0699。為了在頻率 ω PWM下獲得相同的衰減,將極數相乘,電阻器除以 FSF = ω PWM /ω。當然,至少可以說,這些電阻器和 1 F 電容器使用起來不方便。因此,我們可以選擇一個阻抗比例因子 ZSF,例如 10 -8乘以電容并劃分電阻。結果為 37.0k(選擇接近的標準值)和 10n。(應用 ZSF 對濾波器的響應沒有影響。)已知 1 Ω / 1 F 濾波器的極點并要求 h( ) = F,求根例程也為我們提供了 t s = 32.5 s 的值。將 t s除以 FSF 保持相同的 F 并導致 t s的值等于 12.01 ms。
當然,沒有理由期望 R’s 和 C’s 相等會產生一個濾波器,在給定的 F 值下產生盡可能低的 t s和 ω PWM。我們應該如何尋找更好的濾波器?我們使用蒙特卡洛。從上面極點的 FSF 縮放值開始,只有當它減少 H( , , , ω PWM ) 或 h(, , , t s ) 的值而不增加另一個的值時,才會選擇一個新的、更好的極點集. 運行了一個 1000 萬樣本的蒙特卡羅,其中包含一組隨機選擇的極點。結果是 -2290.7、-2238.9 和 -2218.6 處的極點,更好的紋波衰減 .001938 < F,以及大大改進的 ASE 7.3834?10 -10. 顯然,的選擇是同極,有時也稱為同步極。不幸的是,不可能用圖 1 的網絡實現同步極點。但是如果我們設置 R 3 = K?R 2 = K 2 ?R 1和 C 1 = K?C 2 = K^2C 3 ,我們可以接近,其中 K 是一個大于 1 的值。K越大越好。當然,K 的值有明顯的實際限制,但讓我們看看 K 為 1、√10、10、100 和無窮大的情況。參見圖 2,它顯示了滿足“標準”的濾波器的時域響應。
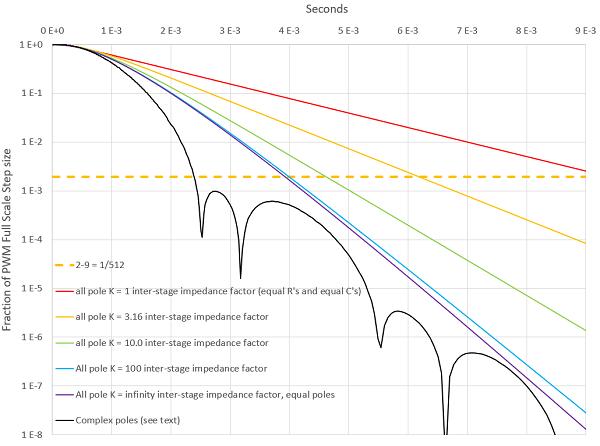
圖 2 ASE 顯示了各種濾波器類型的滿量程 PWM 轉換與時間的關系。水平線對應于 2 -9的 ASE 。
水平虛線的值為 F = 2 -9。其他每條曲線對應于 H( , , , ω PWM ) 也為 F 的濾波器的 ASE。曲線在濾波器的 ASE 降至 F 時與水平線相交。表現差的是紅色曲線,其中對于 K = 1,R 和 C 相等。對于 K = √10 和 10,黃色和綠色更好并且看起來實用,但是藍色 K = 100 濾波器需要 K 2 = 10000 的阻抗比。紫色 K = 無窮大曲線是無法實現的……或者是嗎?
圖 1 網絡的濾波器在驅動阻性負載時會降低精度。簡單的解決方案是在電壓跟隨器配置中使用運算放大器緩沖它們的輸出。使用此運算放大器還有另一大優勢:圖 3中的濾波器配置擴展了可實現的濾波器類型的數量,不僅包括等極點版本,還包括性能更好的濾波器——通過反復試驗確定的復雜極點濾波器,從貝塞爾濾波器的極點開始。“更好”的極點是:-.84668、-.786203+.725726?√-1 和 -.786203-.725726?√-1。該濾波器的 R 值可以縮放,使其衰減 H( , , , ) 在 ω PWM是 F。縮放濾波器的性能由黑色曲線反映。為什么奇怪的形狀?復數極點產生由阻尼振蕩組成的時間響應。它在穩定時反復通過零。圖中顯示的是響應的。
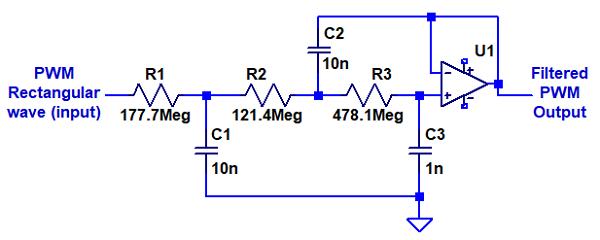
圖 3可以實現實極點(部分或全部相同)和復極點的濾波器結構圖像。對于顯示的組件值,表 1 的復數極部分的每個給定行中的參數值都得到滿足(見正文)。
您可能認為這些圖顯示了復極點濾波器的先天優勢。但它們僅代表 F = 2 -9滿足“標準”的情況。F 的其他值呢?其他值為 ω PWM的 PWM 又如何呢?這是一個答案。PWM 具有整數位數,因此僅當 N 是一組正整數時,才考慮 F = 2 -N的值才有意義。對于每個 2 -N和每個正在考慮的過濾器,我們可以確定滿足“標準”的 ω 和 t s的值。知道 ω 后,可以為任何所需的 PWM ω PWM計算 FSF ,FSF 也可以用于確定縮放 t s的值和過濾器 R’s。在具有 FSF 標度極點的濾波器中,ω標度= FSF?ω 和 t s-標度= t s /FSF。因此,無論 PWM 頻率 ω PWM為何,ωPWM與 FSF 縮放的 t s的乘積將保持不變。這個產品的價值越小越好。我們可以針對復數濾波器和同步濾波器比較這些產品,以確定哪個是每個 F 值的更好選擇。請參閱表 1。
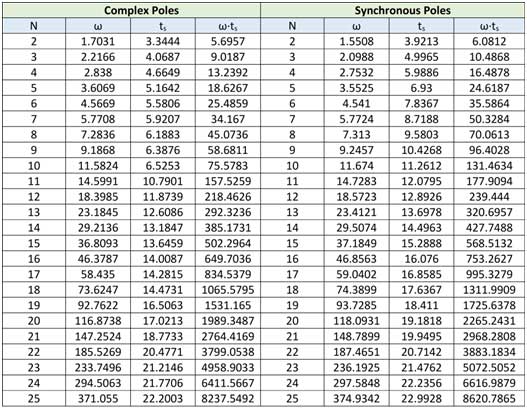
表 1對于各種 F = 2 -N值,復雜同步濾波器的ω、t s和 ω?t s的值。
比較表明,對于每個 F,復濾波器具有更小的值乘積,是更好的選擇。我們現在可以概括濾波器設計過程。
實施解決方案
一個具體的例子將說明一般問題的解決方案。假設一個 PWM,其中 B = 8 且 T = 2 B /1 MHz = .000256。我們想要 F = 2 -9的紋波電平和 ASE 。圖 3 顯示了表 1 中復雜濾波器的濾波器元件值。對于 N = 9,濾波器給出頻率 ω = 9.1868,對應 F 值。但我們希望衰減頻率為 ω PWM = 2π /T。我們需要將濾波器的電阻器和表的 t s = 6.3876 除以 FSF = ω PCM /ω = 2671.7。由此得出 R1 = 66.527 kΩ、R2 = 45.445 kΩ 和 R3 = 178.95 kΩ(您可以使用接近的標準值)和 t s= 2.39 毫秒。您也可以選擇通過恒定 ZSF 縮放這些電容器和電阻器,將電阻器乘以該值并將電容器除以該值。ZSF 操作對濾波器響應沒有影響。
應該注意的是,對于 N = 6 或更小的值,同步濾波器具有比復數濾波器更小、更好的 ω 值,并且對于更大的 N 值,ω 的值幾乎相同。盡管如此,復雜的過濾器仍然是更好的選擇;可以使用表中對之間的分母中的 ω 值計算 FSF。增大 ω 會增加紋波衰減和穩定時間。總能找到一個 FSF 值,它會導致 ω 和 t s的縮放濾波器值比其他濾波器提供的值更小。
為任意頻率的 PWM 設計濾波器
已經提出了一種使用運算放大器和三對電阻器和電容器的方法來設計用于任意頻率和位數的 PWM 的濾波器。該濾波器將 ASE 和峰值紋波限制為 F,即用戶選擇的負整數 2 的冪。研究了具有各種相互關系的極點的濾波器。所選的復極點濾波器在所考慮的濾波器中具有的頻率和穩定時間乘積。使用表 1 和圖 3,對于任何頻率的 PWM,濾波器組件可以縮放到所需的 F 值。可以對表中列出的穩定時間應用相同的縮放比例,以計算縮放后的穩定時間。
如果您更喜歡無運算放大器的解決方案,您可能需要考慮圖 1 電路的 K = 10 版本。在 R1 = 4.3k 和 C1 = 100n 的情況下,對于 F = 2 -9,您在圖 2 中的綠色曲線中看到的 t s約為 4.6 ms。對于相同的 F,該濾波器的 ω 為 15787 弧度/秒。我尚未提供此濾波器的表格,但您可以在將不同的 FSF 應用于濾波器電阻器時在電路模擬器中測試結果。
免責聲明:本文為轉載文章,轉載此文目的在于傳遞更多信息,版權歸原作者所有。本文所用視頻、圖片、文字如涉及作品版權問題,請聯系小編進行處理。
推薦閱讀:
如何設計用于牲畜監測、車隊管理和工業 4.0 物流的多重連接跟蹤系統
助推成渝雙城經濟圈建設,第十一屆中國(西部)電子信息博覽會強勢來襲





