【導讀】波特圖也是根據人名命名的,它是出自貝爾實驗室,由荷蘭裔科學家 Hendrik Wade Bode在1930年發明的。Bode當時需要設計用于電話網絡的放大器,放大器帶有負反饋。為了能夠快速了解放大器保持絕對穩定所需的增益裕度和相位裕度,Bode開發了波特圖。
為什么要學習波特圖呢?
波特圖將傳輸函數和頻率響應定性的聯系起來了,通過波特圖的繪制,可以了解極點和零點是怎么影響頻率響應的幅度和相位,進而影響電路的性能。 換成人話,可以這樣說。 波特圖也是根據人名命名的,它是出自貝爾實驗室,由荷蘭裔科學家 Hendrik Wade Bode在1930年發明的。Bode當時需要設計用于電話網絡的放大器,放大器帶有負反饋。為了能夠快速了解放大器保持絕對穩定所需的增益裕度和相位裕度,Bode開發了波特圖。 假設一系統為線性時不變系統,傳輸函數為H(s)。則波特圖有兩副圖,幅頻圖和相頻圖,分別對應增益和相位。 幅頻圖是|H(s=jw)|隨頻率的函數,其橫軸為頻率,用對數尺度表示;縱軸為功率的dB值,即20log10|H|。 相頻圖是arg(H(s=jw))隨頻率的函數,其橫軸為頻率,用對數尺度表示;縱軸的單位一般為度,為線性值。 畫幅頻圖時,遵循以下規則: (1) 當頻率w經過極點時,|H(jw)|的斜率變為-20dB/dec,也就是以頻率變化10倍,|H(jw)|變小20dB; (2) 當頻率w經過零點時,|H(jw)|的斜率變為20dB/dec,也就是以頻率變化10倍,|H(jw)|變大20dB; (3) 圖在起始點時的增益值,可以計算頻率的下限值對應的|H(jw)|; 如果零點沒有在原點處的時候,可以將w=0代入|H(jw)|,計算其在DC處的增益; 如果有零點處在原點處,則可以選擇一個靠近w=0的值,比如說w=1作為|H(jw)|的初始值。零點在原點,即w=0時,|H(jw)|=0,因為縱軸是對數值,所以不可能在圖中包括|H(jw)|=0的值。 什么是波特圖?
怎么畫波特圖?
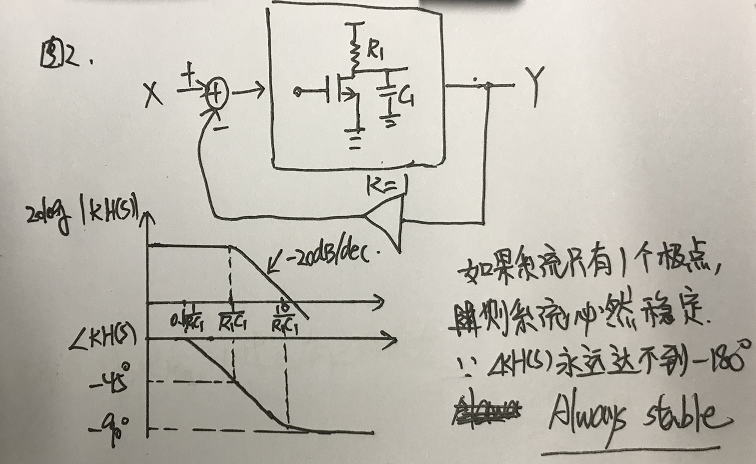
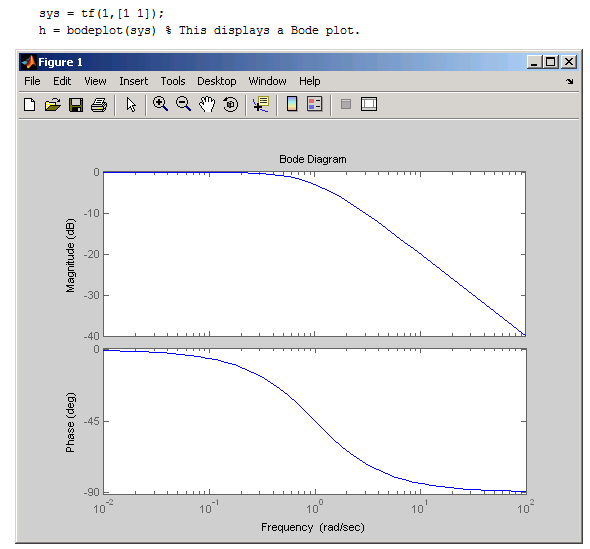
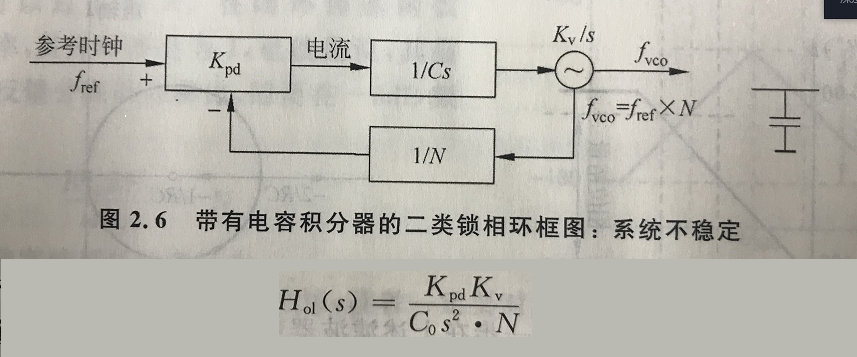
(4) 圖在起始點的斜率,取決于在w小于起始點處零點和極點的個數,然后按照(1)和(2)的規則計算;如果在w小于起始點處無零點和極點,則初始斜率為0。 畫相頻圖時,遵循以下規則: (1) 假設極點為wp,即其則曲線在0.1wp處開始變化,在wp處變化-45度,在10wp處變化接近于-90度。 (2) 假設零點為wz,則曲線在0.1wz處開始變化,在wz處變化45度,在10wz處變化接近于90度。 看到電路,快速畫出波特圖,了解系統的穩定性 當K等于0時,沒有反饋,此時系統為開環系統; 當K不等于0時,此時系統為閉環系統。 其中,KH(s)稱為環路增益。 由上面等式可知,當KH(jw)=-1時,Y/X-->無窮大,即使X很小很小,也會導致很大的Y輸出,即系統處于振蕩狀態,不穩定。 所以為了保證系統穩定,需要在任何頻率處都不能滿足KH(jw)=-1的條件,即|KH(jw)|=1&arg(H(jw))=-180度。 那如果是|KH(jw)|>1&arg(H(jw))=180度呢? 因為每經過一次環路,信號都會被進一步放大,因為反相,所以疊加出來的信號會變得越來越大。 所以當 |KH(jw)|>=1 arg(KH(jw))=180度, 系統都處于一個不穩定的狀態。 用圖形示意,可能會比較直觀。 增益等于0dB對應的頻率,稱為gain crossover frequency. 相位等于-180度對應的頻率,稱為phase crossover frequency. 若系統穩定,則要求gain crossover frequency<phase crossover frequency. 舉兩個例子,解釋一下,如何從電路到波特圖,再分析系統的穩定性。 所以,如果電路只包含一個極點的話,那么這個系統肯定是穩定的。 可以看到,系統中相應部件對最后波特圖的影響,比如說,原來系統處于不穩定的狀態,但是當降低K的值時,系統則會變穩定。 增益裕度和相位裕度都是衡量系統穩定程度的方法。 在相位圖上,找到相位達到-180度時對應的頻率,然后計算該頻率對應的幅度值。如果|KH(jw)|180>=1,則該系統不穩定;如果|KH(jw)|180<1,則系統穩定。 在波特增益圖上,找到|KH(jw)|=1的頻率,稱為w0dB,然后找到該頻率下KH(jw)w0dB的相位。 如KH(jw)w0dB的相位大于-180度,則系統穩定。 KH(jw)w0dB的相位與-180度之間的差,稱為相位裕度。 一般取相位裕度為60度左右,此時任務系統處于一比較好的穩定狀態。 不想自己手工畫波特圖,怎么辦? 計算機已如此普及,當然可以不用手工畫啦。matlab中有現成的函數。 還有什么可以用到波特圖呢? 當環路濾波器只有一個電容時,如下圖所示。 可以看到環路中只有兩個零極點,所以相位圖為接近-180度的一條直線,因此其總相位裕度基本為0,表面這個鎖相環是不穩定的。 解決問題的一個辦法是給電容加入一個串聯電阻R,這樣就引入了一個零點,從而對環路進行相位補償。 在實際的應用中,需要額外增加電阻電容低通濾波器,以濾掉一些高頻噪聲和電壓波動。其中最簡單的一種是在上述電容電阻兩端再加一個電容C1,通常C1遠小于積分電容C0,如下圖所示。 這就是我們常用的環路濾波器的結構。 參考文獻: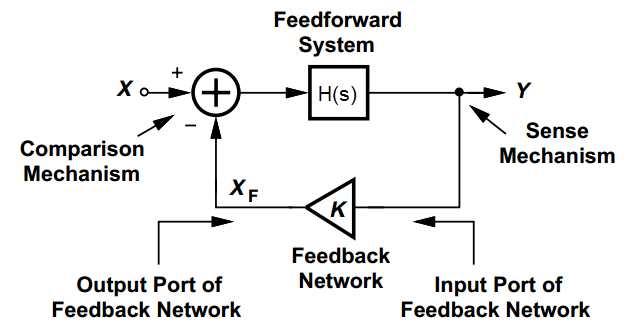
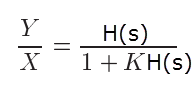
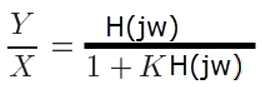


增益裕度和相位裕度



免責聲明:本文為轉載文章,轉載此文目的在于傳遞更多信息,版權歸原作者所有。本文所用視頻、圖片、文字如涉及作品版權問題,請聯系小編進行處理。
推薦閱讀:




